Cryptology: The Science of Secret Codes and Ciphers

This cipher wheel, part of the National Security Agency collection, is similar to one described by Thomas Jefferson. It was used to encode and decode messages.

The word Cryptology comes from the Greek word kryptos, which means hidden and logos, which means word. It is the branch of science that deals with secret communications. To keep communications secret, it is necessary to use a code, a cipher, or both.

A code is a system of symbols representing letters, numbers or words. For example, you could create a code that might represent the following words as:

The=01, in=02, Spain=03, mainly=04, rain=05, falls=06, Germany=07, drops=08, on=09, plain=10

The encoded message might read:

01 05 02 03 06 04 09 01 10.

When you decoded the message by replacing the number with the matching word you get:

The rain in Spain falls mainly on the plain.

Without the table showing what words go with which numbers, it would be very hard to guess the meaning of the encoded message. For this reason codes have been used for thousands of years by people to protect private messages.

Codes are not used only to protect secret information. Certain codes, like Morse Code, were developed before the radio and the telephone to make it easy to send messages great distances. The telegraph allowed a single tone, or beep, to be sent through a wire to a remote location. Morse code translates the letters of the alphabet into a series of short or long beeps. For example, an A is sent as a short beep followed by a long beep. Messages were sent letter by letter across the telegraph wire as many long and short beeps. Morse code could also be used to allow two ships to communicate through the use of blinking signal lights. Even today Morse code is still used in radio because the beeps sometimes can get through heavy static that voice communications cannot.

The table that contains the translation of the words to the code is often in the form of a book and is referred to as a codebook.

A codebook does not need to be a special book filled only with a code. Messages can be passed using any two identical books as long as they contain the words in the message. For example, a spy in country A can send a message to a spy in country B as long as they have the same copy and revision of the book. Take the code:

38-1-1, 213-27-4, 46-22-1

It is meaningless unless you know that the first three numbers represent the page, line and number of words from the left edge in the book Control of Nature by John McPhee. The first three numbers give you the first word of the coded message, the second three numbers the second word, and so on. With this information it is possible to tell that this encoded message is the first three words of:

The rain in Spain falls mainly on the plain.

The fourth word in this message points out a flaw in this system. The book Control of Nature does not contain the word Spain. Any spy would have to find an alternate wording for his message. Even the words that can be found in the book can be difficult to locate, making encoding and decoding time consuming. One way of solving this problem is to use a cipher instead of a code.

Ciphers

A cipher is a system for encoding individual letters or pairs of letters in a message. One of the simplest ciphers was said to have been used by Julius Caesar and for that reason this type of cipher still bears his name. The Caesar cipher shifts letters around. For example, every letter on the left of the equal sign below corresponds to a letter on the right:

A=C, B=D, C=E, D=F, E=G, F=H, G=I, H=J, I=K, J=L, K=M, L=N, M=O, N=P, O=Q, P=R, Q=S, R=T, S=U, T=V, U=W, V=X, W=Y, X=Z, Y=A, Z=B

We refer to the message before it gets encrypted as the plaintext. You could encrypt the plaintext:

Meet you at the corner

By substituting an O for the M, then a G for an E, another G for the E, and so on until the whole message was changed to:

OGGV AQW CV VJG EQTPGT

This is called a substitution cipher. The encoded message is nolonger readable. To make it even harder to understand, the coder can break the letters up into arbitrary groups of five or so (called code groups) with no spaces. Extra meaningless letters are filled in at the end to make the last code group the same length as the others. This hides the length of each of the words in the message. After breaking the above message up into code groups we get:

OGGVA QWCVV JGEQT PGTXY

The Enigma encoding/decoding machine from WWII.

Cryptanalysis

Is the message impossible to read without knowing the secret of the Caesar cipher? No, it isn't. There is another branch of this science known as cryptanalysis. The science of cryptanalysis deals with "breaking" and reading secret codes and ciphers. How would you go about using cryptanalysis to read the above code? The primary tool for this is a frequency list. Each language shows definite patterns in how often certain letters appear in sentences. For example, in English the letters "Q", "X" and "Z" are rarely used while the letter "E" is used the most often. The order of letter frequency in English is:

ETAONRISHLGCMUFYPWBVKXJQZ

with E the most frequent and Z the least used. We could attempt to decode the above message by replacing the most frequently appearing letter in the code with the letter E:

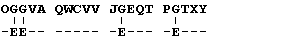
The next most frequently used letter is "T":

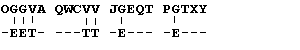
At this point replacing the third most popular letter in the code with the third most frequent letter, "A", would be a problem. In the encoded message the letters Q and T appear twice each. Which is the "A"? While frequency lists provide a guide for decoding a substitution cipher, there are plenty of sentences in English in which "E" is not the most frequent letter. To decode a message it might be necessary to replace any of the frequently used code letters with any of the five most popular English letters in different combinations to see if the resulting sentence has meaning.

We could also try to see if there are any words we can figure out based on the information we have so far. It isn't hard to conclude that the first word of the message is MEET. After all there are only a few words in English where the end part is EET (Other ones include FEET, BEET, BEETLE).

Now things start to get a little more tricky. A cryptoanalyst would substitute the remaining most frequent letters in the code with the most frequent English letters in different combinations working the letters like a puzzle. Eventually the analyst would figure out that the Q and T must be O and R. This would yield:

If we got this far, a little thought would take us to the final message:

MEETY OUATT HECOR NER--

Or correctly spaced:

MEET YOU AT THE CORNER.

The Caesar code is extremely easy to break, because after you discover that G is E and V is T, it is not difficult to conclude that the code works by shifting the letter in the alphabet by three places. More complicated is a substitution cipher where each letter in the alphabet is randomly mapped to the code letters. For example:

ABCDEFGHIJKLMNOPQRSTUVWXYZ

NMZAYBXCWDVEUFTGSHRIQJPKOL

has no simple pattern. The message "Meet you at the corner." With this code becomes:

UYYI OTQ NI ICY ZTHFYH

Another simple cipher uses columnar transposition. With this cipher the message is written out as rows of five letters with no spaces and arranged in columns. So Meet you at the corner becomes:

The cipher is generated by reading the letters off of each column top to bottom then left to right:

MOHNE UEEEA CRTTO XYTRX

Someone understanding the code could reverse the process. To make it even more difficult to break the cipher the way the columns are read off can be controlled by a key. A key is a word or group of letters that is needed to read an encrypted message. For example, the word "THUNDER" could be used to further secure the above message within the columnar transposition cipher. Each letter in the key would be given a number equal to the order in which it appears in the alphabet.

THUNDER

6374125

Then the numbers are lined up over the message placed in the same number of columns as the number of letters in the key. Extra letters are added at the end to make the length come out properly:

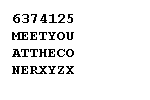
Then the columns are read off in the order of the numbers to make the code:

YEYOC ZETET HXUOX MANETR

Even if you know that the message was encoded using columnar transposition, it will not be easy to decode without the keyword THUNDER which tells how many columns were used and the order in which they were read off into the code.

Still, even this method of coding can be broken by knowing the frequency certain letters appear in a language. To counter this codemakers came up with ciphers that encode letters as pairs. The following method is called digraphic substitution. Let's use this method to encode just the first word of our message: MEET.

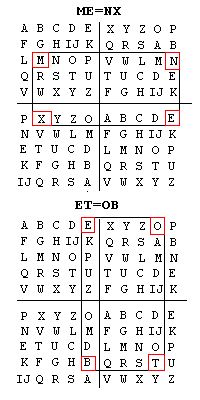To the right are two matrixes of letters. The top left and bottom right quadrants of each matrix have the alphabet written in proper order with I and J sharing the same space to make things come out evenly. The other two quadrants have the alphabets in two different scrambled orders. By taking the first two letters of MEET, ME we can create a box on the matrix with the upper-left at M and lower-right at E (Look at the top matrix). The other corners of the box represent the encoded pair NX. For ET we get the encoded pair OB (Shown on the bottom matrix). Notice that the pair of E's in MEET now are represented by two totally different letters in the code NXOB. This makes the E's hard to find and the code difficult to break.

Encryption and Encoding Devices

All the ciphers we have discussed so far can be encoded and decoded with a pencil and paper. As time went on, mechanical devices were invented to make encryption and decryption easier. One early device used by the Greeks was a rod on which a belt was wrapped on an angle so it covered the rod from end-to-end. A message was written on the belt along the length of the rod. Then the belt was unwound from the stick and worn by the messenger. When the messenger arrived at his destination, he would take off the belt. When it was wound around another rod of the same size the message would reappear.

Thomas Jefferson described a drum-like device that was used to encode and decode messages. Jumbled alphabets ran along rows the length of the device. The coder would pick one row to be the plaintext and read the cipher off another row matching the letters column by column. To decrypt the message the decoder was required to know which number rows had been used.

A clever, but simple device was invented by Sir Charles Wheatstone in 1867. This machine looked like a clock face including the short and long hands. Instead of numbers around the dial there were two alphabets, one running along the outer edge and the other running a little further inside. The outer alphabet was in proper order, while the inside one was jumbled. The hands were connected by gears so that as the person encrypting the message moved the big hand to a plaintext letter, the inner hand moved to the corresponding cipher character. The cipher character was written down, then the long hand moved to the next plaintext letter. The hands were geared so the they did not move at the same rate. This meant that while the first E in a message might correspond to a cipher V, the second E in the message would be a letter different from V. This made figuring out the message by using a frequency list difficult.

By the early part of the twentieth century, electro-mechanical encryption machines were common. One famous device, called THE ENIGMA, was used by the Germans during WWII. Despite it being a fairly complicated machine with many gears, keys and lights, it still used just a series of substitution ciphers one after another to encode messages. By shifting the ciphers by one letter each time a new letter was encoded, the builders of the machine were able to minimize the chance that the frequency of certain letters appearing in the code could be used to break it. Even so, the messages generated by the ENIGMA machines were broken continually by the Allies during the War and many credit this feat of cryptoanalysis with shortening the conflict and saving many lives.

The introduction of computers has revolutionized crytography. Computers can be used to make ciphers far more unbreakable than could ever be done with pencil and paper or even a machine like the ENIGMA. Computers can also be used to break codes that in the past might have seemed unbreakable. So far, it is far easier for a computer to encrypt a message than to break it.

Encryption is no longer the business of just government and spies. The ability to safely encrypt communications is very important to anyone who uses the internet. When somebody purchases from an on-line store, they use a credit card number. The number must be encrypted so that only the store can see it and it cannot be intercepted by third parties that might use the number without the cardholder's permission. Using the type of ciphers we've discussed so far, this would be very difficult to do. The cipher they use would need a key. How could both the computer on the buyer's side and computer on the store's side know the key without sending it across the internet where it could be intercepted?

The solution lies with a type of cipher that can do what is known as public key encryption. These ciphers don't just use one key, but two. One key is used to encrypt a message, the other to decrypt it. The most important feature of this type of cipher is that knowing the encryption key does not help someone to know how to decrypt the message.

The transaction between the buyer and the bookstore would go like this: The store's computer generates a pair of keys (encryption and decryption, more commonly known as public and private keys) and sends the public key to the buyer's computer. The buyer's computer then uses that key to encrypt the message. That message is sent across the internet to the store's computer. The store's computer can then decrypt the message using the private key. Anyone listening in on this transaction would only see the public key and the encrypted message, not enough information to find out what is in the text of the message.

Codes, ciphers and encrypts will continue to play a greater role in our everyday lives as we continue into the 21st century.

Experiment: Build Secret Coding Devices

Copyright Lee Krystek 2000. All Rights Reserved.